お金には交換・計算・保存の3機能の他に、増殖の機能があることを前回みてきました。
<前回投稿>
お金の自己増殖機能|①お金のレンタル料
今回は、お金の自己増殖機能の根幹をなす仕組みである、複利についてみていきます。
指数関数的な増加
池のハスの問題。
「ある池に1日で2倍に増えるハスの葉を浮かべました。ハスの葉が増えていって池の半分を占めるまでに、浮かべた日から数えて50日かかりました。このハスの葉が残り半分も含めて池全体を埋め尽くすのは、何日目になるでしょうか。」
高校数学の教科書でコラム欄に載っていたクイズです。
100日目と答えてしまいそうになりますが間違いです。
50日目に池の半分を占めたハスの葉は、次の日には2倍に増えて池全体を埋め尽くしてしまいます。つまり、答えは51日目です。
この問題は、指数関数的な増加の爆発性を伝えています。
他に有名なものでは、ドラえもんの「バイバイン」という道具で、5分ごとにおまんじゅうが倍になるお話も、指数関数の爆発性と恐ろしさを題材にしています。
(このお話では、増え続けるおまんじゅうを最終的に宇宙に飛ばしてましたが、そんなんで大丈夫なのでしょうかね笑、まあフィクションなので。)
複利の破壊力
お金の世界でも「複利」という指数関数的に増加する仕組みがあります。
投資などで元本に対して〇〇%増えた利益分について、これを再投資します。すると「元本+利益分」があらたな元本となります。
この増えたあらたな元本に対してまた〇〇%が複利で増えていき、これを再投資して、、、というように資産が雪だるま式に増えていきます。
投資は規模の世界です。
100万円を運用して5%増えても5万円の利益ですが、1億円を運用して5%増やすと500万円の利益になります。
複利は元本に対して〇〇%増えるというものなので、増えた分を再投資することで元本が増え続けます。元本が増え続けるということは、複利が効いて増える分がどんどん加速していくことになります。
複利の凄まじさを教えてくれる、「ジャックとジル」というアメリカで有名な話があります。以下動画(ショート)が非常にわかりやすいため、掲載させていただきます。
「投資の神様」の資産推移
「投資の神様」ともいわれる投資家ウォーレン・バフェットの資産額は、2020年に90歳を超え10兆円規模になっています。
彼自身は質素で倹約家であり、その投資スタイルには、多くの個人投資家が見習うべき点が多々あります。今回は本題ではないので、また別の機会に譲るとします。
そして興味深いことに、彼の資産額の99%は、彼が50代以降に築いたものになります。
この凄まじさを感じるのに、以下動画(ショート)が非常にわかりやすいため、掲載させていただきます。
彼の資産は、50歳から90歳の40年間でざっくり100倍になっていて、とてつもなく素晴らしい成績にみえます。
しかし、この「40年間で100倍」を年リターンに換算すると実は12%くらいになります。
つまり、年平均リターン12%を40年継続すると、元本は約100倍になるということです。
年平均リターン12%はそれなりに良い成績ではあるものの、飛び抜けて素晴らしい成績とまでは言えません。しかし、これは超長期で投資を継続してきた賜物といえるでしょう。
参考までに、複利〇%で40年間運用した場合に、元本が何倍になるのかをグラフに示したものが以下になります。
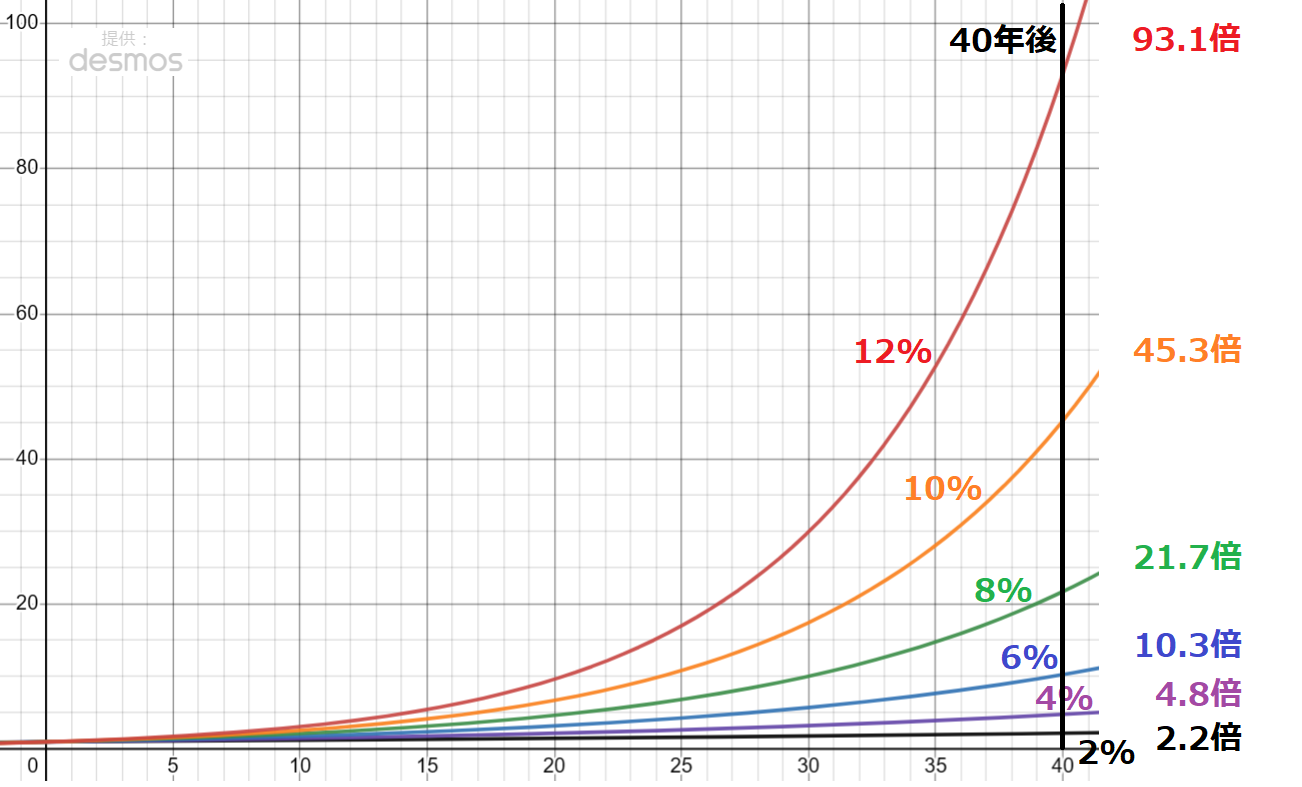
このグラフや前節の「ジャックとジル」のお話、本節のウォーレン・バフェットの例からも分かりますが、複利の破壊力を最大限に引き出すのは時間です。
どれだけ長期にわたって投資を継続できるか、どれだけ早くから投資を始められるかが重要であることがわかります。
まとめ
複利の仕組みは、数学でいうところの指数関数に対応し、その増え方の破壊力をいくつかの例で見てきました。
もちろん投資の世界で絶対はないので、毎年かならず〇〇%で増えるなんてことはあり得ません、その年によってはマイナスにもなります。
しかし、中期・長期・超長期で適切な投資を継続した場合には、「平均」して年リターン数%以上の実現は十分現実的です。
この破壊力に囚われて、すべてのお金を投資に突っ込んでしまうこと、今に使えるはずだったお金を先延ばしにしていることに他なりません。
将来のための投資・貯蓄と今のための消費、適切なバランスでマネープランを考える必要がありますね。

コメント