時代の流れもあって、最近、投資を始めたもしくは投資について興味をもって調べ始めた人も多いのではないでしょうか。
新NISAでもiDeCoでも資産運用のシミュレーションでは、必ずと言っていいほど「複利」の考え方が出てきます。
今回は、複利の計算の際に、よくプロのフィナンシャルプランナーの方も使う「72の法則」についてみていきます。
「72の法則」
複利の計算は、一般に単純な掛け算のような暗算では難しいです。
しかし、資産運用の世界では、複利で「元本が2倍になるのに何年かかるか」をざっくり計算する「72の法則」というものが有名です。
計算は非常に簡単です。
<72の法則>
72÷「複利年率(%)」=「2倍になるまでの年数」
72÷「2倍にするまでの年数」=「必要な複利年率(%)」
例えば、複利3%であれば72÷3=24で、24年で元本が2倍程度になると計算できます。
また反対に、8年で元本を2倍にしたければ72÷8=9で、必要な複利年率は9%程度と計算することもできます。
さらに、以前の投稿で挙げたグラフでも、いくつか試してみましょう。
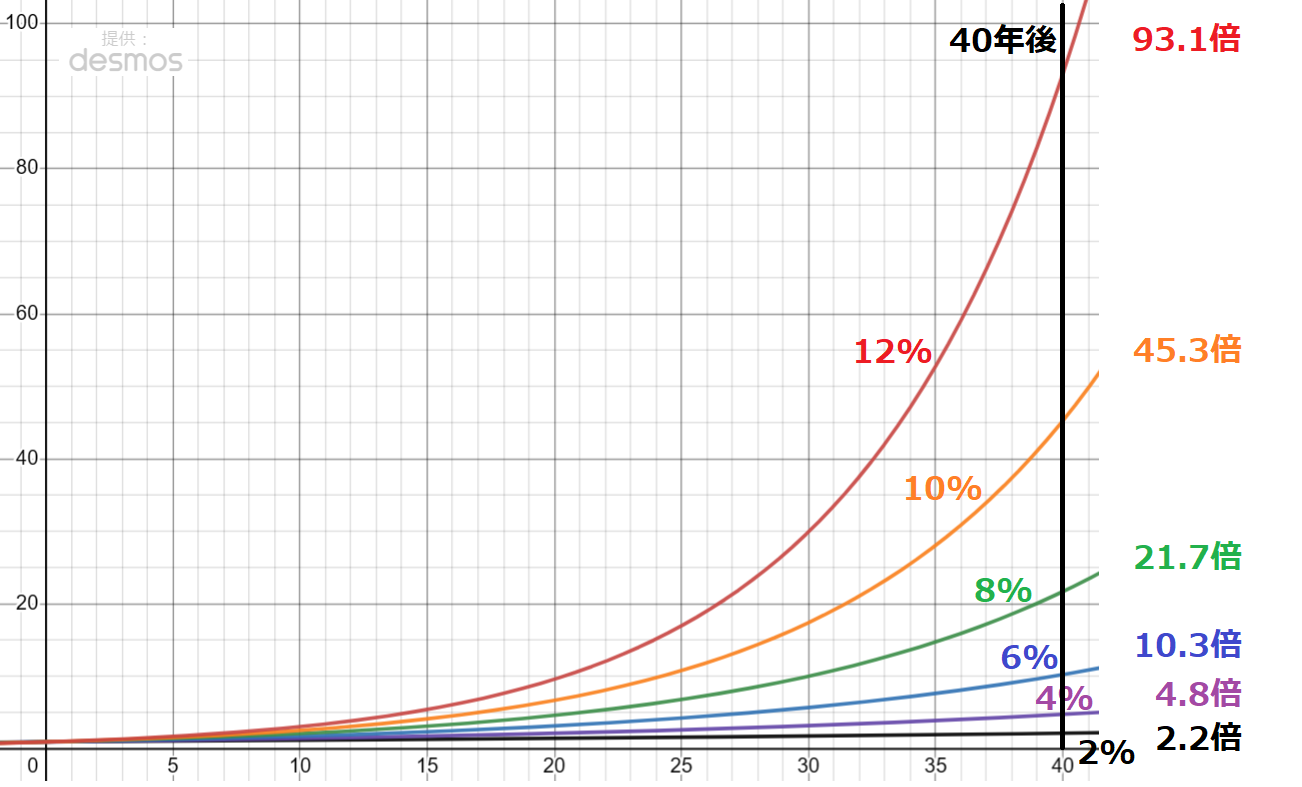
見やすい場所を基準にするため、複利8%(緑)のグラフで、30年時点で縦軸10(倍)程度となっている点(30,10)を始点にしましょう。
すると、その資産が2倍の20(倍)に到達する期間は、72÷8(%)=9(年)と計算できます。
実際に複利8%(緑)のグラフが、20(倍)に達するのは、横軸39(年)あたりなので、基準とした(30,10)から9年後あたりに、2倍になっていることが確認できます。
ダメ押しでもう1つ。
複利12%(赤)グラフの(30,30)を基準にして、2倍の60(倍)に達するのは、72÷12(%)=6(年)と計算でき、グラフでも横軸36(年)あたりで、縦軸60(倍)になっていることとおよそ一致しています。
<参考投稿>
「72の法則」のカラクリ
少し数学に足を踏み入れますが、この「72の法則」は高校数学の範囲で次のように示すことができます(近似の部分のみ一般に大学数学の範囲であるマクローリン展開を使っています)。

上記のように、一番近いのは「69」の法則ですが、暗算で割り算する際には約数が多い「72」の方が便利であるため、「72の法則」として定着したのでしょう。
上記の証明を利用すれば、2倍だけでなく、1.5倍や3倍などの法則を次のように作ることが可能です。
・1.5倍になる → 「40~42の法則」 (ln1.5=40.55…)
・2倍になる → 「69~72の法則」 (ln2=69.31…)
・3倍になる → 「108~110の法則」 (ln3=1.098…)
積み立てながら運用する場合
「72の法則」も万能ではありません。
この法則は「元本を複利のみで増やしていったときが前提」であって、積立投資のように「追加で原資を増やしながら(もしくは反対に取崩しながら)複利で運用していった場合」には使えないのです。
このようなシナリオで、それなりにちゃんと計算する場合は、フィナンシャルプランナー(FP)3級などで出てくる、
・年金終価係数
・減債基金係数
・資本回収係数
・年金現価係数
などを駆使する必要があります。
しかし、ネットにたくさんシミュレータが転がっているので、以下のようなものを使うと簡単に計算ができます。
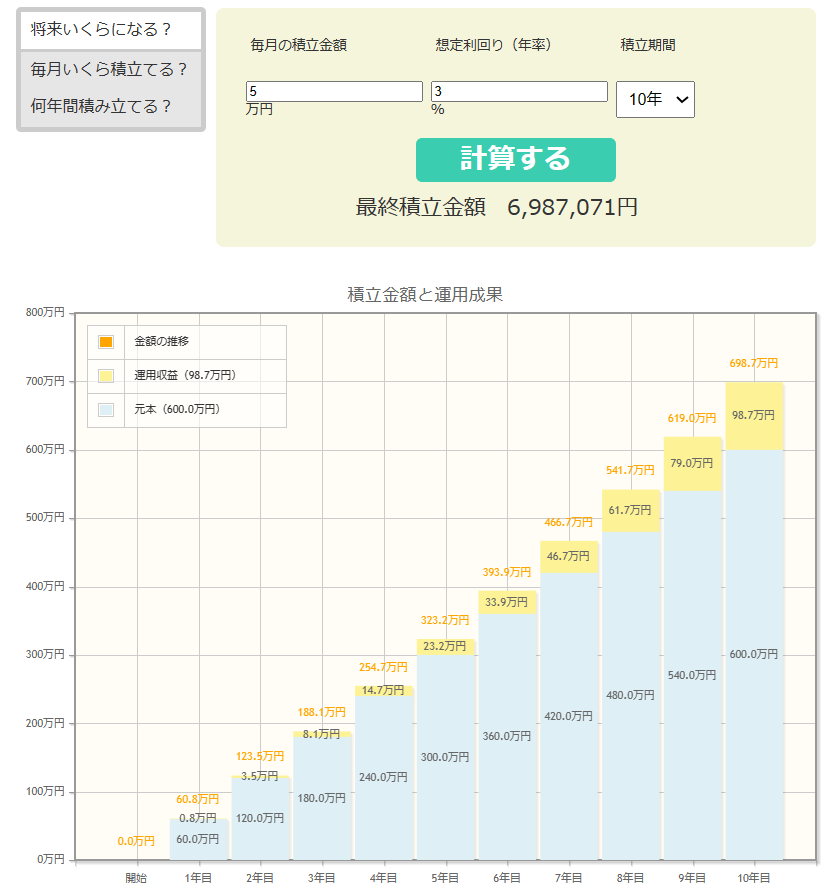
https://www.fsa.go.jp/policy/nisa2/moneyplan_sim/index.html
まとめ
投資・資産運用の世界で必ず付きまとう複利の計算の際に、簡単な暗算をサポートする「72の法則」について見てきました。
その中身を数学を使ってのぞいてみると、状況によって「70」を使った計算でも問題ないことがわかり、より柔軟性が増した知識として理解できたのではないでしょうか。
仕組みがわかれば応用ができる、これが学びを加速させる秘訣ですね、それこそ複利のごとく指数関数的に(笑)。


コメント